2018, Vol. 3, Issue 2, Part F
Theoretical concept of linear higher and algebraic equations
Author(s): Roji Lather
Abstract: This paper contributes to the theoretical analysis of linear Differential Algebraic Equations of higher order as well as of the regularity and singularity of maÂtrix polynomials. An algebraic number field is a finite extension field of the field of rational numbers. Within an algebraic number field is a ring of algebraic integers, which plays a role similar to the usual integers in the rational numbers.Some invariants and condensed forms under appropriate equivalent transformations are given for systems of linear higher
-order Differential
-Algebraic Equations’ with constant and variable coefficients. Inductively, based on condensed forms the original Differential
-Algebraic Equations system can be transformed by differentiation
-and
-elimination steps into an equivalent strangeness
-free system, from which the solution behaviour (including consistency of initial conditions and unique solvability) of the original Differential
-Algebraic Equations system and related initial value problem can be directly read off. It is shown that the following equivalence holds for a Differential
-Algebraic Equations system with strangeness
-index ^ and square and constant coefficients. For any consistent initial condition and any right
-hand side
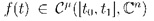
the associated initial value problem has a unique solution if and only if the matrix polynomial associated with the system is regular.
Pages: 434-442 | Views: 1478 | Downloads: 14Download Full Article: Click Here

How to cite this article:
Roji Lather. Theoretical concept of linear higher and algebraic equations. Int J Stat Appl Math 2018;3(2):434-442.

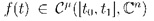 the associated initial value problem has a unique solution if and only if the matrix polynomial associated with the system is regular.
the associated initial value problem has a unique solution if and only if the matrix polynomial associated with the system is regular.
