2016, Vol. 1, Issue 1, Part A
Relations between the degrees of transitive constituents of G1 and the absolutely irreducible constituents of permutation representation G* of the group G
Author(s): B Razzaghmaneshi
Abstract: Let be a finite set of arbitrary elements, G be permutation group on Ω, Δ ⊆ Ω, G
1 = {1} = Δ
1, Δ
2,..., Δ
n are n orbits of G, n
i = |Δ
i|, f
i is the degree of different irreducible representation of D
1…D
r appearing in G
*, V=V(G) be the ring of all the matrices of G, dimV=k. And also if the irreducible constituents of permutation representation G* are all different, then the expression
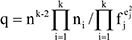
is a rational integer.
Pages: 22-26 | Views: 2344 | Downloads: 32Download Full Article: Click Here

How to cite this article:
B Razzaghmaneshi. Relations between the degrees of transitive constituents of G1 and the absolutely irreducible constituents of permutation representation G* of the group G. Int J Stat Appl Math 2016;1(1):22-26.

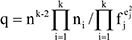 is a rational integer.
is a rational integer.
